How Do You Know How Large to Make Error Bars on a Histrogram?
The geom_errorbar() function
Error bars give a general idea of how precise a measurement is, or conversely, how far from the reported value the true (mistake gratis) value might be. If the value displayed on your barplot is the upshot of an aggregation (similar the mean value of several data points), you may want to display error bars.
To understand how to build it, you commencement demand to empathise how to build a bones barplot with R. Then, you merely it to add together an extra layer using the geom_errorbar() function.
The function takes at to the lowest degree iii arguments in its aesthetics:
-
yminandymax: position of the lesser and the top of the fault bar respectively -
10: position on the X axis
Note: the lower and upper limits of your fault bars must be computed before building the chart, and available in a column of the input data.

# Load ggplot2 library(ggplot2) # create dummy data data <- data.frame( name=messages[one : 5], value= sample(seq(iv,fifteen),5), sd= c(1,0.2,3,2,4) ) # Most bones error bar ggplot(data) + geom_bar( aes(x=proper name, y=value), stat= "identity", fill= "skyblue", alpha= 0.7) + geom_errorbar( aes(x=proper name, ymin=value-sd, ymax=value+sd), width= 0.four, color= "orange", alpha= 0.ix, size= 1.iii) Customization
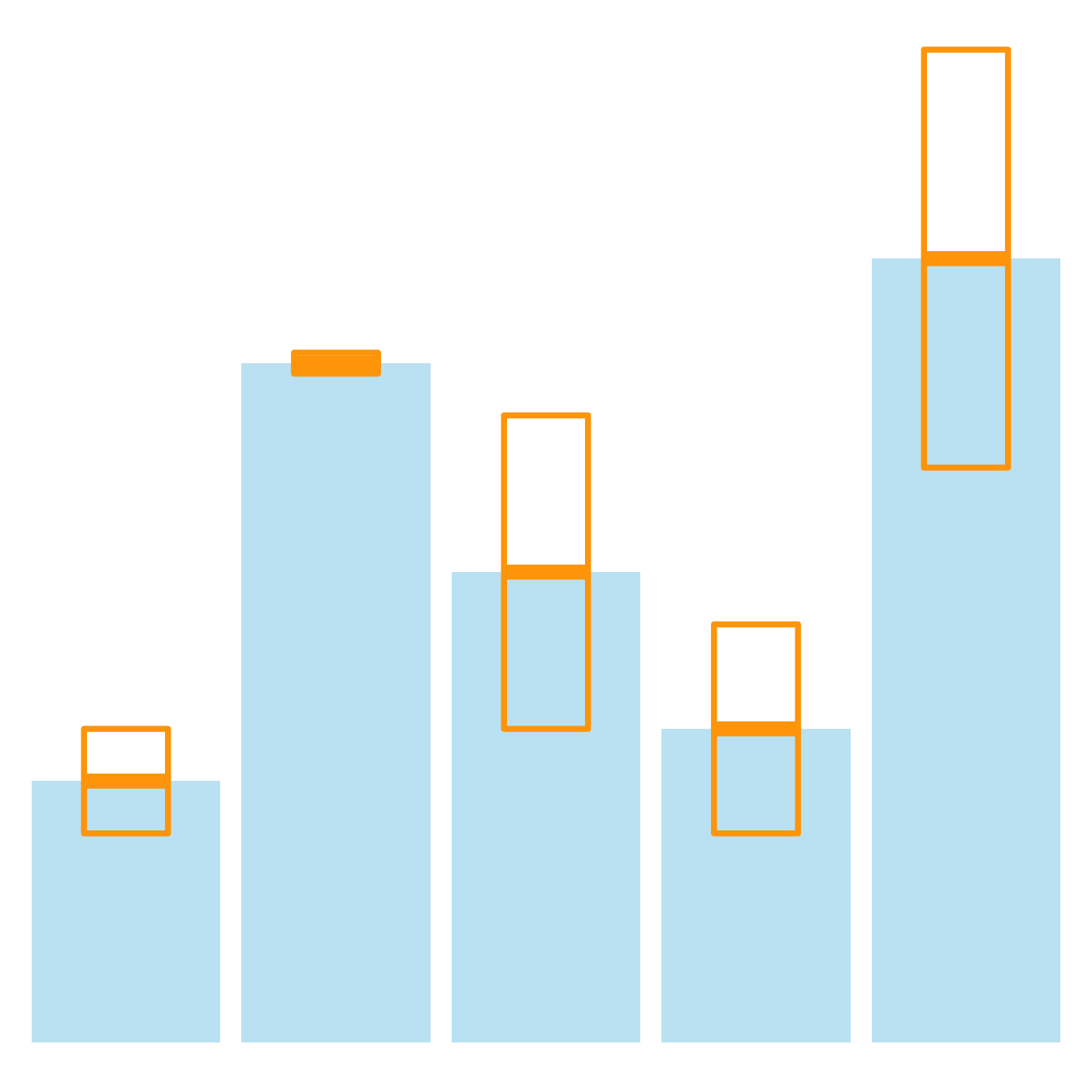
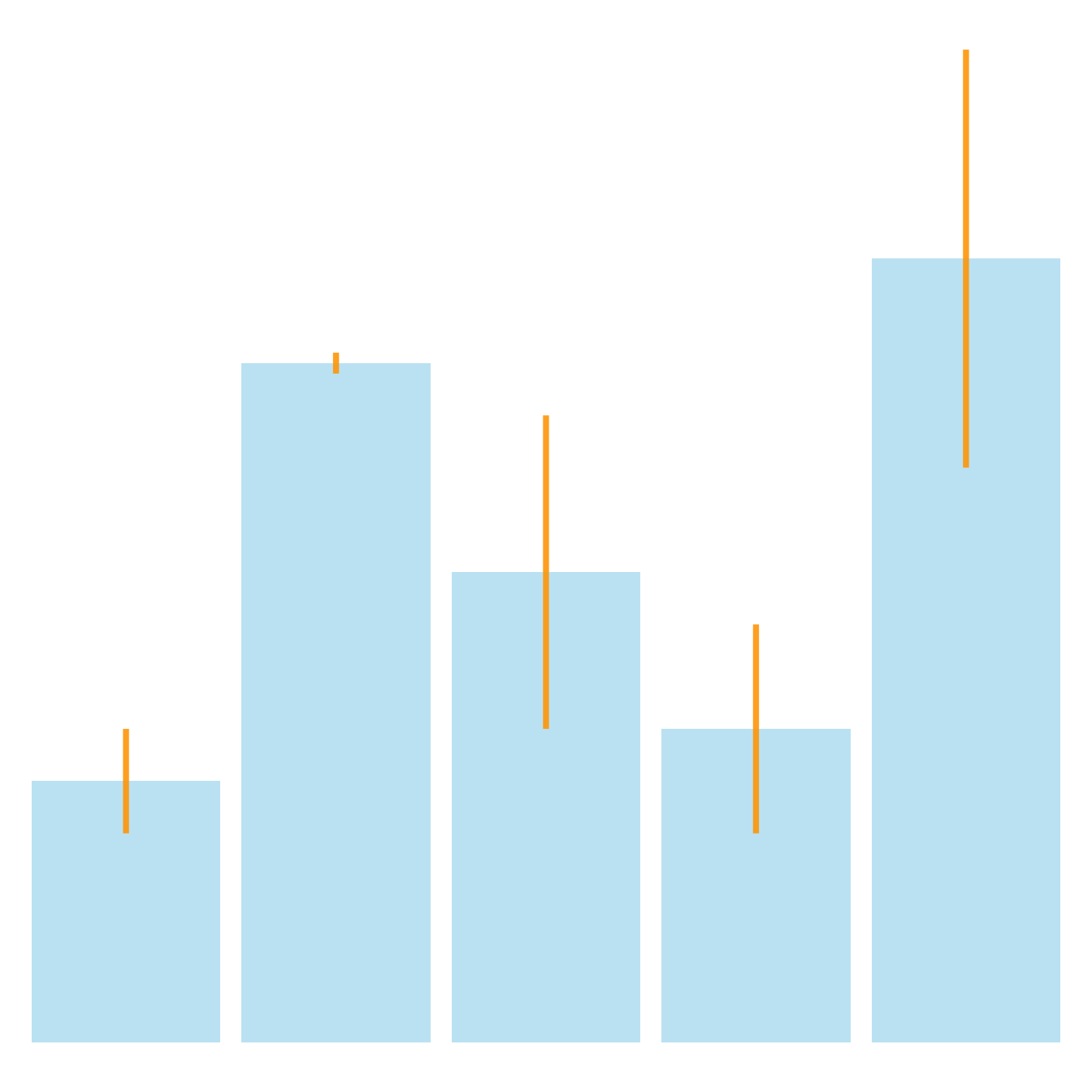
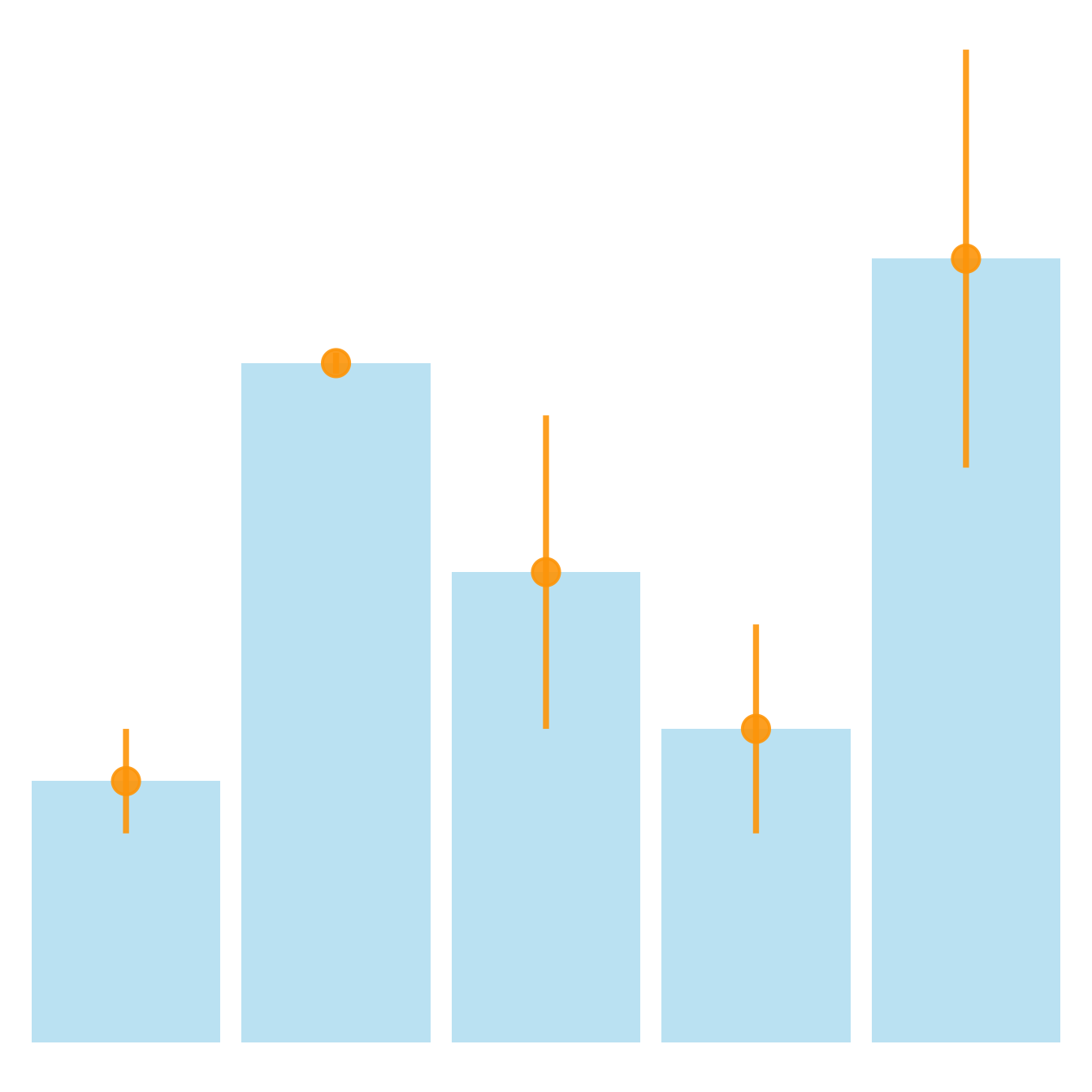
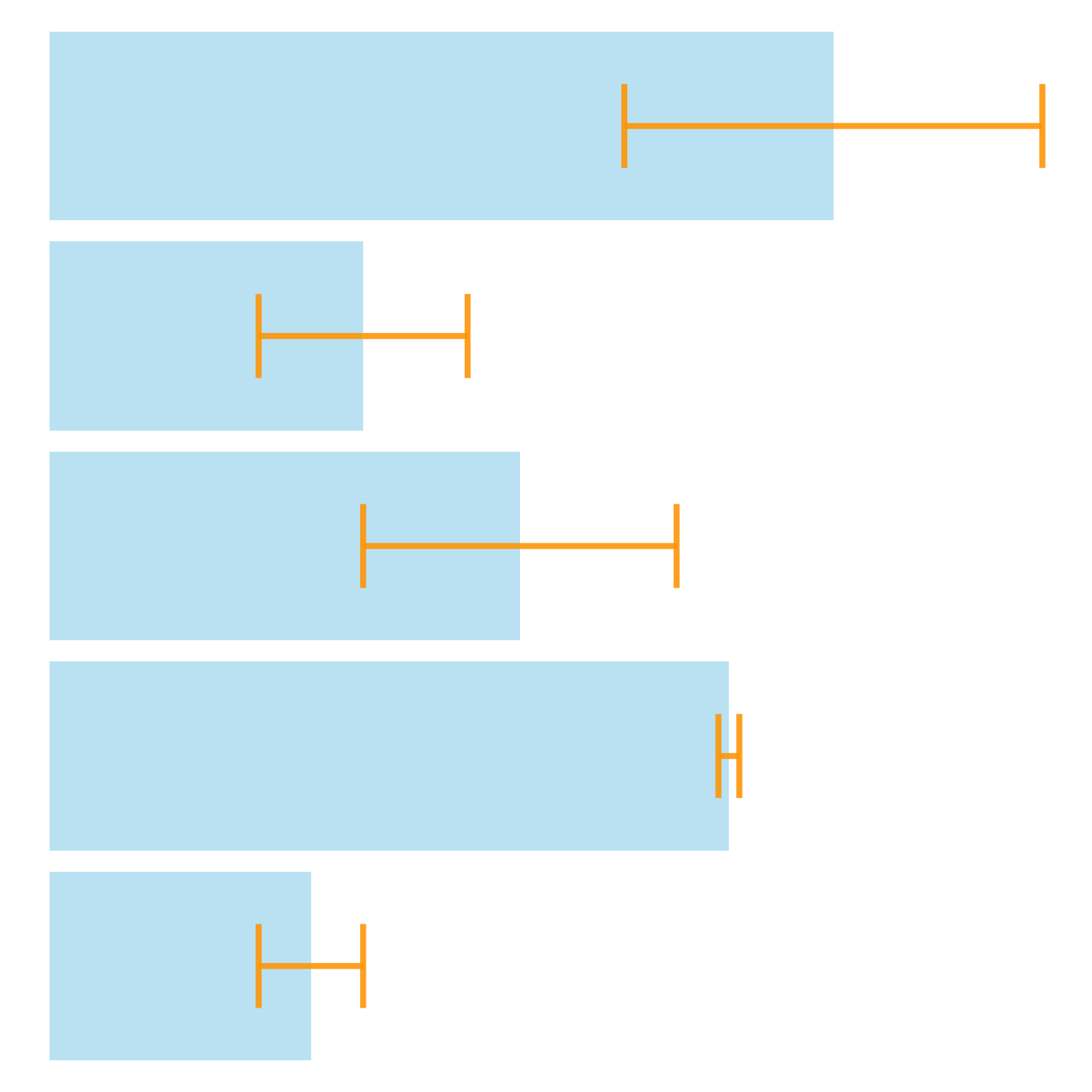
It is possible to modify error bar types thanks to like part: geom_crossbar(), geom_linerange() and geom_pointrange(). Those functions works basically the same every bit the most common geom_errorbar().
# Load ggplot2 library(ggplot2) # create dummy data data <- information.frame( name=letters[ane : v], value= sample(seq(4,15),5), sd= c(i,0.2,three,2,4) ) # rectangle ggplot(data) + geom_bar( aes(x=proper noun, y=value), stat= "identity", fill= "skyblue", alpha= 0.5) + geom_crossbar( aes(ten=name, y=value, ymin=value-sd, ymax=value+sd), width= 0.4, colour= "orange", alpha= 0.9, size= 1.3) # line ggplot(data) + geom_bar( aes(x=name, y=value), stat= "identity", fill= "skyblue", blastoff= 0.5) + geom_linerange( aes(ten=name, ymin=value-sd, ymax=value+sd), colour= "orange", alpha= 0.9, size= 1.3) # line + dot ggplot(information) + geom_bar( aes(x=name, y=value), stat= "identity", fill= "skyblue", alpha= 0.five) + geom_pointrange( aes(10=name, y=value, ymin=value-sd, ymax=value+sd), colour= "orange", alpha= 0.9, size= one.3) # horizontal ggplot(data) + geom_bar( aes(x=proper name, y=value), stat= "identity", fill= "skyblue", alpha= 0.5) + geom_errorbar( aes(10=name, ymin=value-sd, ymax=value+sd), width= 0.4, colour= "orangish", alpha= 0.9, size= 1.3) + coord_flip() Standard departure, Standard fault or Confidence Interval?
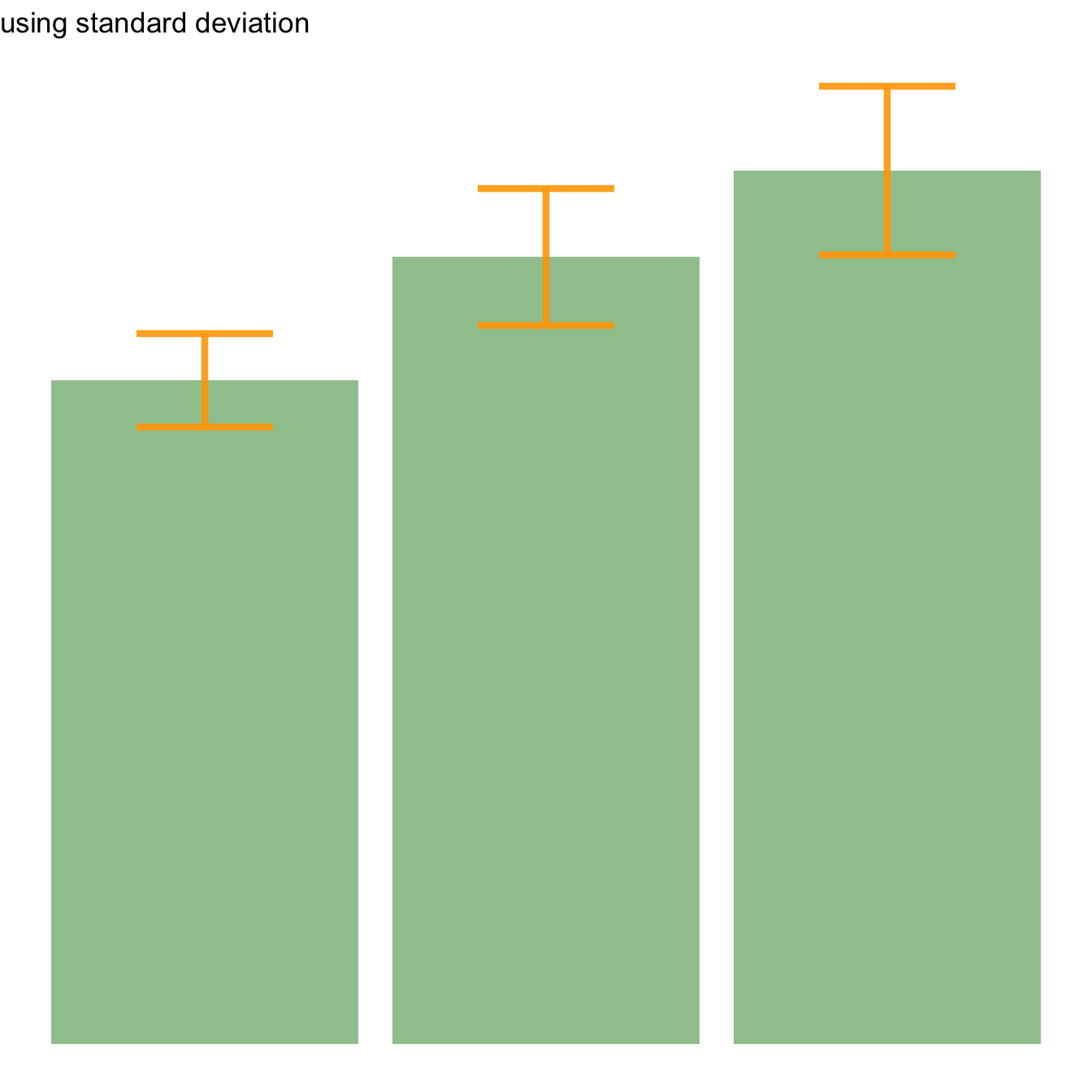
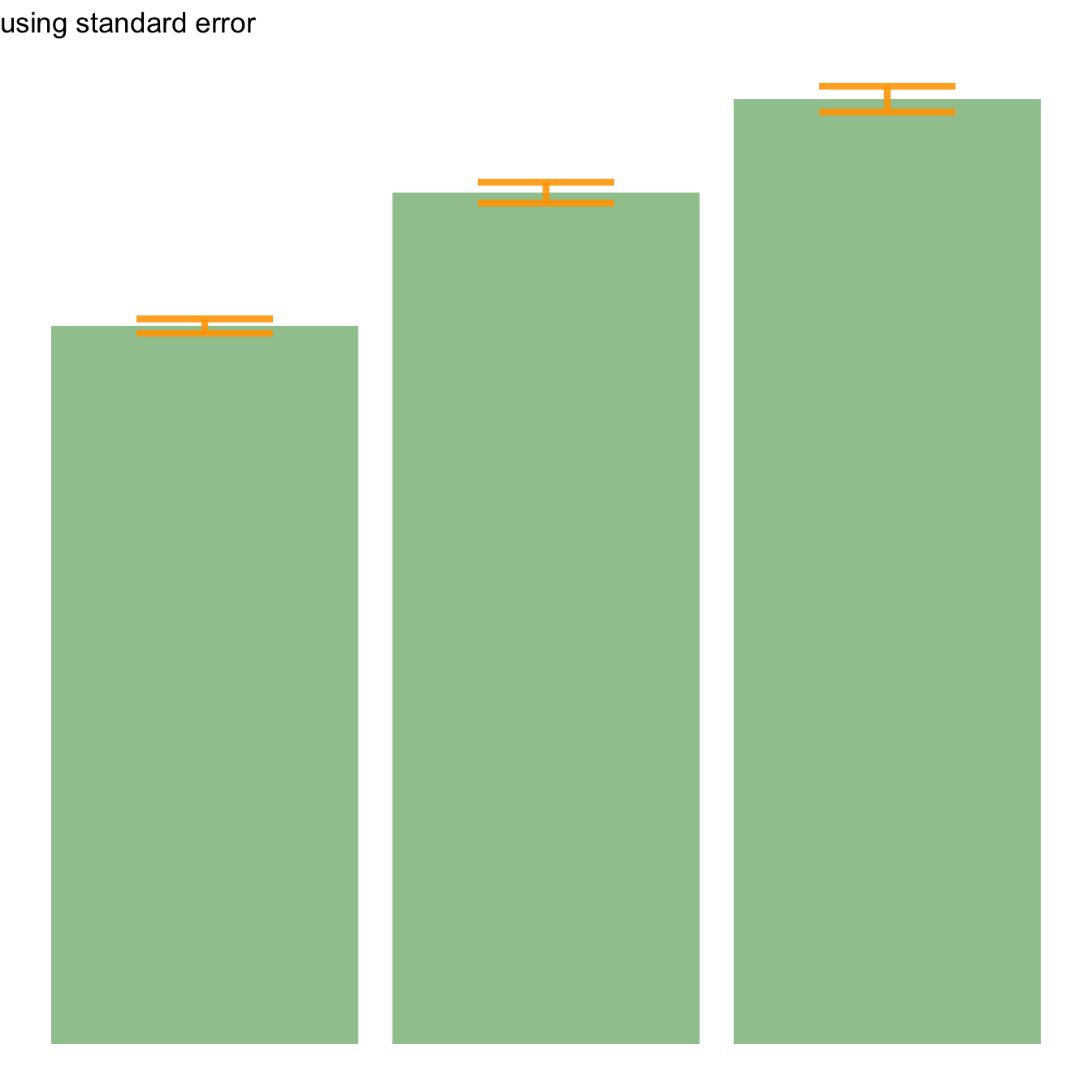
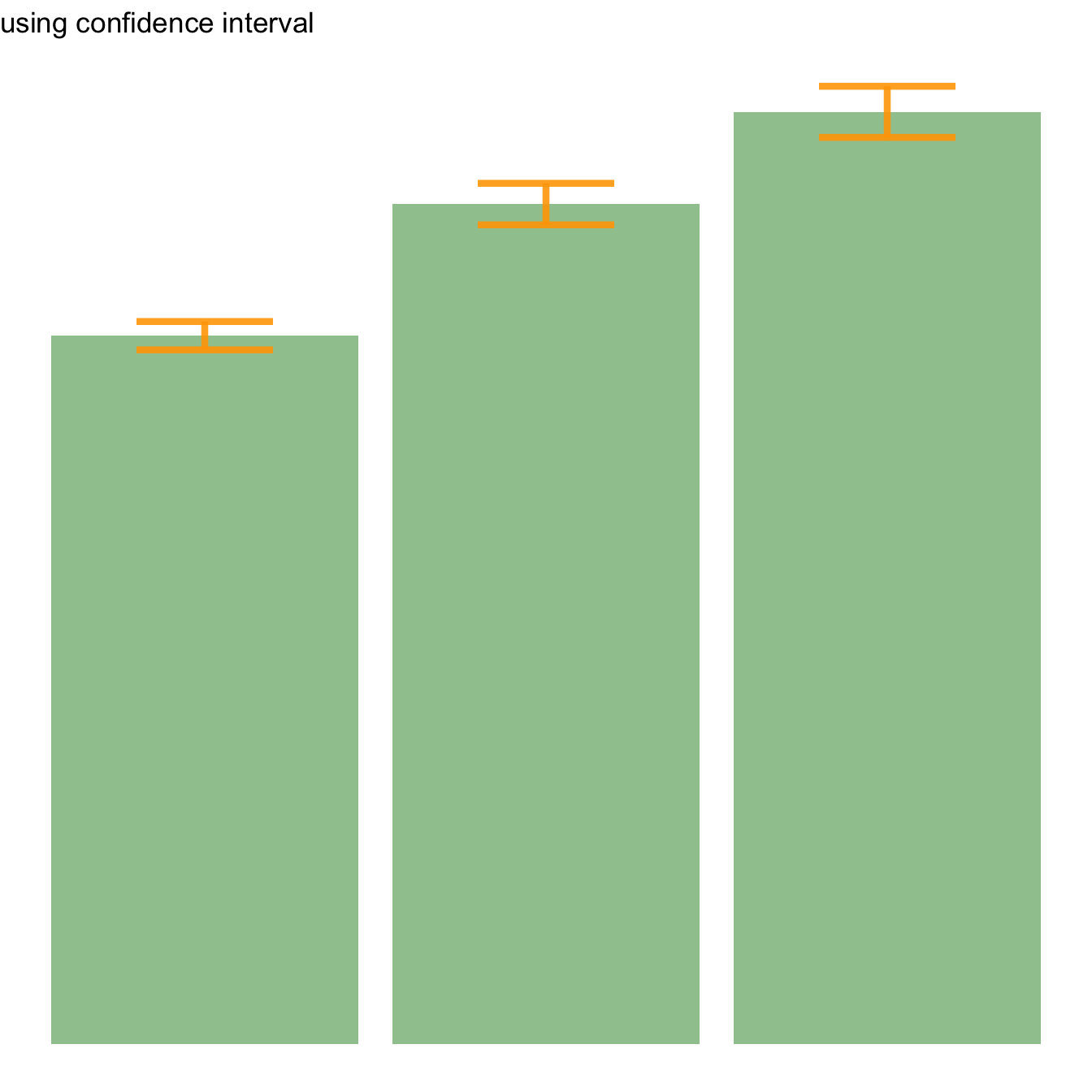
Three different types of values are usually used for error bars, sometimes without even specifying which one is used. It is important to understand how they are calculated, since they give very different results (come across above). Let's compute them on a uncomplicated vector:
vec=c(ane,3,five,ix,38,seven,2,4,9,xix,19) → Standard Deviation (SD). wiki
It represents the corporeality of dispersion of the variable. Calculated every bit the root square of the variance:
→ Standard Mistake (SE). wiki
It is the standard deviation of the vector sampling distribution. Calculated as the SD divided by the foursquare root of the sample size. By structure, SE is smaller than SD. With a very big sample size, SE tends toward 0.
→ Confidence Interval (CI). wiki
This interval is defined so that there is a specified probability that a value lies inside it. It is calculated every bit t * SE. Where t is the value of the Student???s t-distribution for a specific alpha. Its value is often rounded to ane.96 (its value with a big sample size). If the sample size is huge or the distribution non normal, it is better to calculate the CI using the bootstrap method, nevertheless.
Afterward this short introduction, here is how to compute these 3 values for each grouping of your dataset, and utilise them as error bars on your barplot. As you can see, the differences can profoundly influence your conclusions.
# Load ggplot2 library(ggplot2) library(dplyr) # Information data <- iris %>% select(Species, Sepal.Length) # Calculates mean, sd, se and IC my_sum <- data %>% group_by(Species) %>% summarise( north= n(), hateful= mean(Sepal.Length), sd= sd(Sepal.Length) ) %>% mutate( se=sd/ sqrt(n)) %>% mutate( ic=se * qt((1 -0.05)/ ii + .5, n-1)) # Standard departure ggplot(my_sum) + geom_bar( aes(10=Species, y=mean), stat= "identity", fill= "forestgreen", alpha= 0.5) + geom_errorbar( aes(x=Species, ymin=hateful-sd, ymax=mean+sd), width= 0.4, colour= "orange", alpha= 0.nine, size= 1.5) + ggtitle("using standard difference") # Standard Fault ggplot(my_sum) + geom_bar( aes(10=Species, y=mean), stat= "identity", fill up= "forestgreen", alpha= 0.5) + geom_errorbar( aes(10=Species, ymin=mean-se, ymax=mean+se), width= 0.4, colour= "orange", alpha= 0.ix, size= 1.5) + ggtitle("using standard fault") # Conviction Interval ggplot(my_sum) + geom_bar( aes(x=Species, y=hateful), stat= "identity", make full= "forestgreen", alpha= 0.v) + geom_errorbar( aes(10=Species, ymin=mean-ic, ymax=mean+ic), width= 0.4, colour= "orangish", alpha= 0.9, size= 1.5) + ggtitle("using confidence interval") Basic R: use the arrows() function
It is doable to add fault bars with base R only likewise, simply requires more work. In whatever case, everything relies on the arrows() office.
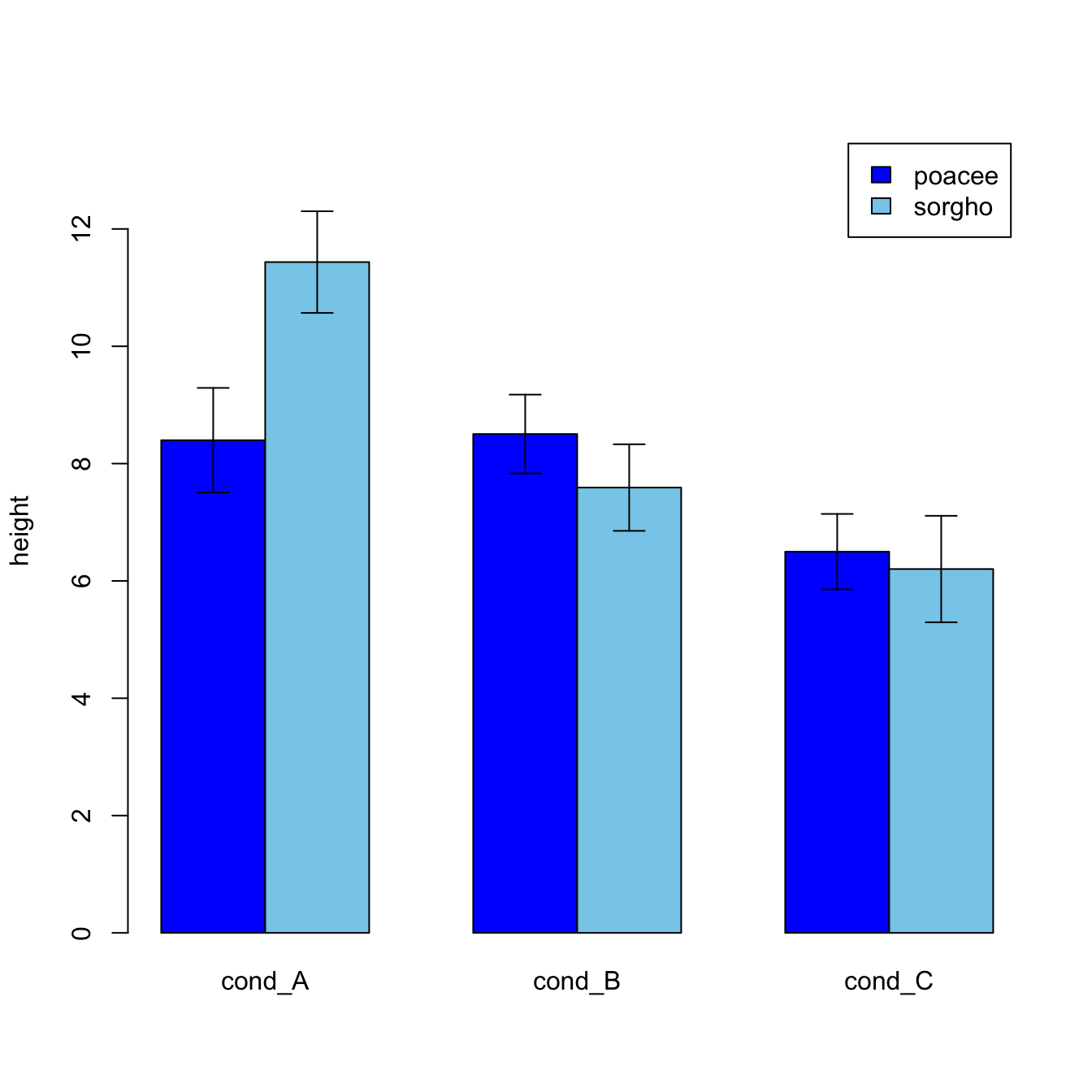
#Let's build a dataset : height of 10 sorgho and poacee sample in 3 environmental conditions (A, B, C) data <- data.frame( specie= c(rep("sorgho" , ten) , rep("poacee" , ten) ), cond_A= rnorm(xx,x,4), cond_B= rnorm(twenty,8,three), cond_C= rnorm(20,v,4) ) #Let's calculate the boilerplate value for each condition and each specie with the *aggregate* function bilan <- amass(cbind(cond_A,cond_B,cond_C)~specie , data=data , mean) rownames(bilan) <- bilan[,1] bilan <- as.matrix(bilan[,- i]) #Plot boundaries lim <- 1.2 * max(bilan) #A function to add arrows on the chart error.bar <- function(x, y, upper, lower=upper, length= 0.ane,...){ arrows(x,y+upper, x, y-lower, angle= 90, code= three, length=length, ...) } #So I calculate the standard divergence for each specie and condition : stdev <- aggregate(cbind(cond_A,cond_B,cond_C)~specie , data=data , sd) rownames(stdev) <- stdev[,1] stdev <- as.matrix(stdev[,- 1]) * 1.96 / 10 #I am ready to add the mistake bar on the plot using my "fault bar" function ! ze_barplot <- barplot(bilan , beside=T , fable.text=T,col= c("blue" , "skyblue") , ylim= c(0,lim) , ylab= "height") mistake.bar(ze_barplot,bilan, stdev) What's side by side?
This post was an overview of ggplot2 barplots, showing the bones options of geom_barplot(). Visit the barplot section for more:
- how to reorder your barplot
- how to utilize variable bar width
- what about error bars
- round barplots
Source: https://www.r-graph-gallery.com/4-barplot-with-error-bar.html
0 Response to "How Do You Know How Large to Make Error Bars on a Histrogram?"
Post a Comment